Dynamika bryły sztywnej
Zadanie 1. Bloczki
Na rysunku poniżej pokazany jest układ dwóch bloczków, na które nawinięta jest nierozciągliwa nić. Bloczek dolny porusza się w dół rozwijając nić, która odwija się z górnego bloczka. Bloczek dolny ma moment bezwładności I1, promień R1 oraz masę m. Górny bloczek ma moment bezwładności I2 i promień R2. Z jakim przyspieszeniem porusza się środek masy dolnego bloczka?
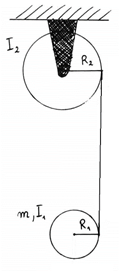
Rozwiązanie:
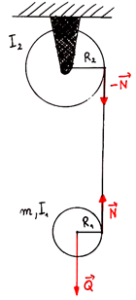
Zaznaczamy na rysunku siły działające na układ bloczków. Przyjmujemy zwrot osi obserwacji ku dołowi i zapisujemy trzy równania ruchu. Jedno na siłę wypadkową środka masy dolnego bloczka, a drugie i trzecie na moment siły działającej na bloczki.
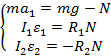
Moment siły dla drugiego bloczka jest ujemny, bo wywołuje ruch zgodny z ruchem wskazówek zegara. Bloczek dolny natomiast obraca się pod wpływem wypadkowego momentu siły przeciwnie do ruchu wskazówek zegara. Przyspieszenia kątowe obu bloczków są różne, co wynika z różnych przyspieszeń stycznych.
![]()
![]()
Przyspieszenie a1 to przyspieszenie środka masy m, a2 to przyspieszenie styczne górnego bloczka. To przyspieszenie styczne jest również przyspieszeniem linki. Zatem przyspieszenie styczne dolnego bloczka jest sumą przyspieszenia bloczka pierwszego i linki.
Wstawiamy przyspieszenia kątowe do układu równań dynamicznych.
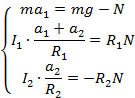
Drugie równanie dzielimy przez R1, a trzecie przez R2.
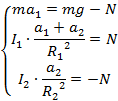
Powyższy układ posłuży do wyznaczenia przyspieszenia dolnego bloczka. Do niego będą się odnosić kolejne przekształcenia. W pierwszej kolejności mnożymy drugie równanie układu przez dwa.
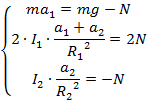
Widać, że teraz możemy pozbyć się jednej niewiadomej (naprężenia nici) poprzez dodanie wszystkich równań do siebie.
![]()
![]()
![]()
![]()
Po podzieleniu obustronnie przez masę otrzymamy wyrażenie, które numerujemy (1), bo jeszcze do niego wrócimy.
(1) ![]()
Teraz odejmujemy od siebie równanie pierwsze i trzecie z naszego układu równań dynamicznych. W tym przypadku również zredukuje się naprężenie.
![]()
![]()
![]()
Dzielimy przez masę m i otrzymujemy wyrażenie na a1.
![]()
W związku z tym, że szukamy przyspieszenia dolnego bloczka a1, dokonujemy przekształcenia tak, aby otrzymać wyrażenie opisujące a2 za pomocą a1.
![]()
(2) ![]()
Otrzymane równanie (2) wstawiamy do (1).
![]()
Wymnażamy każdy składnik nawiasu przez czynnik stojący przed nawiasem i porządkujemy.
![]()
![]()
![]()
![]()
Mnożymy powyższe równanie przez ![]() .
.
![]()
Wyrażenia w nawiasach sprowadzamy do wspólnego mianownika.
![]()
Mianowniki po obu stronach ulegną skróceniu.
![]()
Dzieląc przez pierwszy nawias otrzymujemy wyrażenie na szukane przyspieszenie.
(3) ![]()
Nie jest to najprostsza postać. Zawsze staramy się zapisać wynik tak, aby wyrażenie miało jak najmniej elementów. W tym celu dzielimy mianownik przez nawias z licznika.
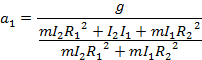
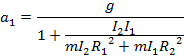
Jeszcze raz wykonujemy podobną procedurę i ostatecznie dostajemy najprostszą postać.
(4) ![]()
ODP. Przyspieszenie środka masy dolnego bloczka wyraża się wzorem (3) lub (4).
Zadanie 2. Drabina
Drabina o długości l = 3 m i masie m = 4 kg oparta jest jednym końcem A o chropowatą, pionową ścianę. Zaś drugim końcem B o chropowatą poziomą podłogę. Współczynniki tarcia w punktach A i B wynoszą odpowiednio 0,1 i 0,2. Ciężar na drabinie rozłożony jest równomiernie. Wyznacz minimalny kąt dla którego drabina nie zsunie się.
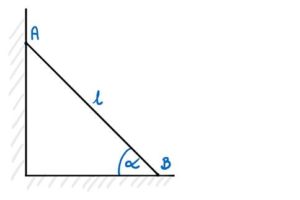
Rozwiązanie:
Zapisujemy wszystkie informacje zawarte w zadaniu.
l = 3 m, m = 4 kg, µ1 = 0,1, µ2 = 0,1, α = ?
Kąt zawiera się w przedziale od 0 do 90 stopni, ponieważ leżąca bądź stojąca pionowo drabina jest rozwiązaniem oczywistym. W pierwszym przypadku jest to równowaga trwała a w drugim chwiejna. Szukamy więc kąta ostrego.
Na rysunku zaznaczamy wszystkie działające na drabinę siły, zachowując mniej więcej proporcję długości.
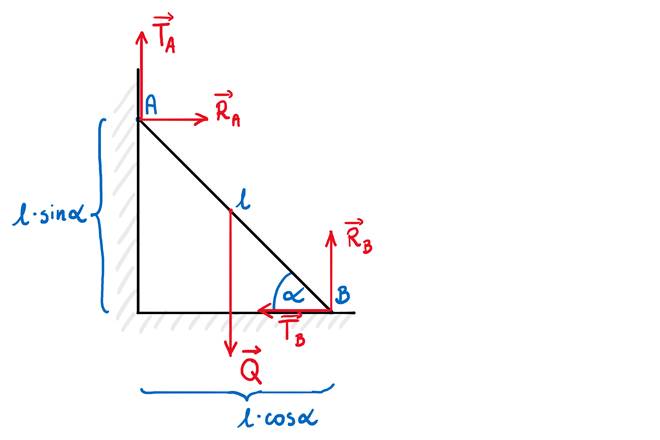
Warunkiem równowagi jest brak siły wypadkowej i brak wypadkowego momentu siły. Nasuwa się pytanie względem jakiego punktu obrót ma nie występować. Oczywiście moment siły musi wynosić zero względem dowolnego punktu. Idealnymi punktami są punkty podparcia A i B, bo ułatwi to rozwiązanie zadania.
![]()
![]()
![]()
![]()
Powyższe warunki zerowania się sił wypadkowych oznaczają, że środek masy drabiny nie przesuwa się ani w poziomie ani w pionie. Dwa ostatnie warunki wykluczają obrót drabiny względem punktu A i B.
Korzystając z ostatniego rysunku uzupełniamy wszystkie te zależności i rozwiązujemy jako układ czterech równań.
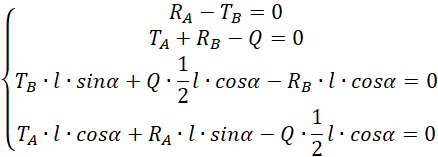
Dwa ostatnie równania dzielimy przez l.
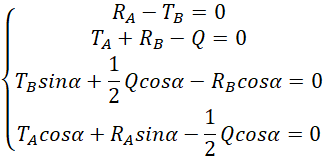
We wszystkich równaniach występuje tarcie, które jest równe iloczynowi współczynnika tarcia i siły reakcji w danym punkcie.
![]()
![]()
Nasz układ wygląda teraz tak:
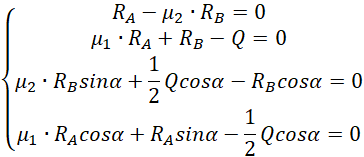
Trudniejsze rozwiązanie:
Wyznaczamy najpierw wyrażenie na reakcję w punkcie A i wstawiamy w odpowiednie miejsca.
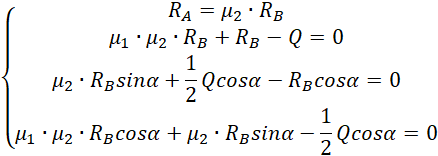
Z drugiego równania wyznaczamy wzór na reakcję w punkcie B.
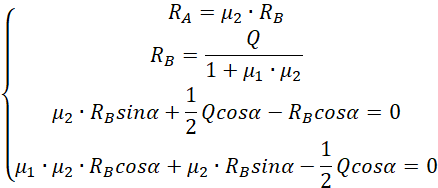
Otrzymane wzory wstawiamy do dwóch ostatnich równań układu.
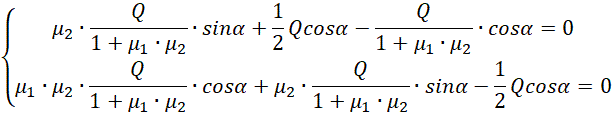
Rozwiążmy równanie pierwsze z dwóch powyższych.
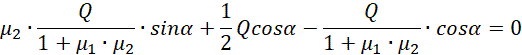
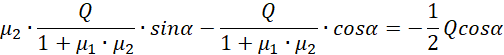
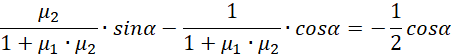
Możemy podzielić równanie obustronnie przez cosinus ponieważ rozwiązanie z pionowo stojącą drabiną jest trywialnym rozwiązaniem.
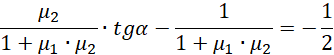
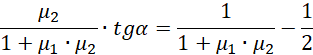
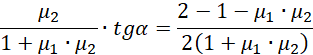
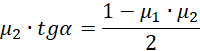
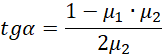
Taki sam wynik uzyskamy z drugiego równania (polecam sprawdzić). Pozostało podstawić dane i odkryć wartość kąta granicznego.
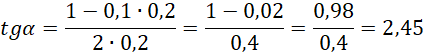
![]()
Prostsze rozwiązanie:
Prostsze rozwiązanie i na pewno szybsze uzyskamy, gdy wyznaczymy obie reakcje z ostatnich równań i podstawimy do pierwszego równania.
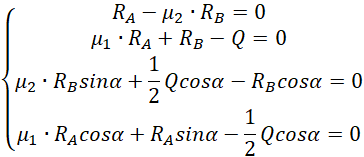
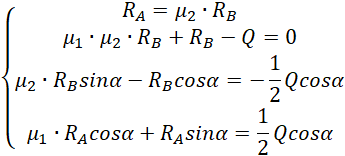
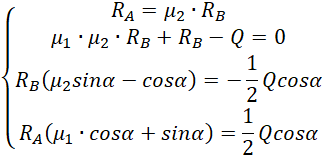
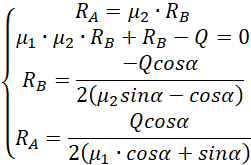
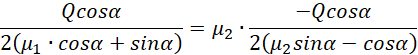
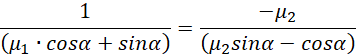
![]()
Dzielimy przez cosinus, bo nie tracimy żadnego rozwiązania. Pionowo stojąca drabina czyli cosinus równy zeru jest rozwiązaniem trywialnym i na pewno nie minimalnym.
![]()
![]()
![]()
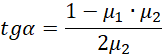
Jak widać sposób powyższy jest zdecydowanie najkrótszy.
ODP. Minimalny kąt oparcia drabiny o ścianę (mierzony do poziomu) wynosi około 67,8°.
