Zasada zachowania pędu i energii
Zadanie 1. Zderzenie niesprężyste z wagą.
Kawałek plasteliny o masie m spada z wysokości h na szalkę wagi sprężynowej. Masa szalki to M, a współczynnik sprężystości wynosi k. Napisz równanie opisujące zależność prędkości od wartości odkształcenia sprężyny. Przyjmij, że plastelina przylepiła się do szalki wagi.
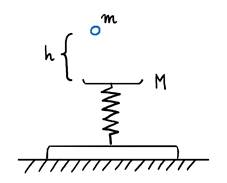
Rozwiazanie:
Najlepiej zacząć od narysowania wagi, która jest jeszcze nieobciążona szalką M. Jako x0 oznaczymy wychylenie początkowe sprężyny tuż przed uderzeniem kulki m o szalkę M. W tym momencie na szalkę działają dwie siły: grawitacji i sprężystości. Jeżeli szalka była przed uderzeniem w spoczynku, to obie się równoważą.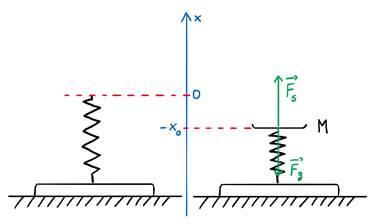
Tuż po uderzeniu plasteliny o szalkę M odkształcenie jest prawie takie samo jak w chwili gdy była tylko szalka. Można dla tej sytuacji zapisać wyrażenie na energię całkowitą układu. Energię potencjalną sprężystości i potencjalną grawitacji będziemy liczyć względem x = 0.
![]()
Jako vk rozumiemy prędkość z jaką szalka, wraz z przyklejoną plasteliną, ruszy tuż po uderzeniu. Wyznaczymy ją z zasady zachowania pędu. Przypominam, że w zderzeniach niesprężystych niespełniona jest zasada zachowania energii. Kulka przylepia się do szalki i dlatego jest to sytuacja niesprężysta. Natomiast x0 obliczymy z warunku równowagi siły sprężystości i siły grawitacji.
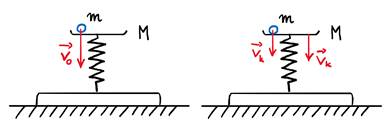
Na rysunku powyżej widać dwie sytuacje graniczne zderzenia niesprężystego. Lewy rysunek to chwila przed przyczepieniem się plasteliny m do szalki M. Prędkość na tym rysunku jest prędkością końcową spadku z wysokości h. Na prawym rysunku natomiast widać chwilę po uderzeniu. Prędkość uzyskana w chwili uderzenia jest prędkością szalki jak i kulki.
Zapisujemy zasadę zachowania pędu dla tego zdarzenia i wyznaczamy vk.
![]()
![]()
W tym równaniu przeszkadza nam nieznajomość prędkości v0. W tym przypadku można do obliczenia zastosować zasadę zachowania energii. Podczas spadania energia potencjalna plasteliny zamienia się na energię kinetyczną w chwili zderzenia.
![]()
![]()
![]()
![]()
Możemy teraz zapisać ostateczną postać prędkości początkowej plasteliny i szalki.
![]()
W naszym wyrażeniu na początkową energię układu nie mamy określonego początkowego odkształcenia x0. Zapisujemy warunek równowagi sił, który pozwala znaleźć brakujące wyrażenie.
![]()
![]()
![]()
Podczas dalszej części ruchu zmiana położenia i prędkości powoduje zmianę wyrażenia określającego całkowitą energię układu.
![]()
Jeżeli układ jest wyizolowany od wpływu otoczenia (np. brak oporów ruchu), to energia całkowita nie ulega zmianie. Początkowe wyrażenie na energię E0 można przyrównać do Ec. Pamiętajmy o podstawieniu wcześniej wyliczonych elementów x0 oraz vk.
![]()
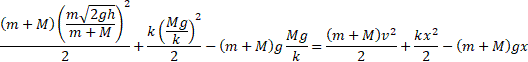
![]()
![]()
Uzyskane równanie mnożymy obustronnie przez 2 i dzielimy przez sumę mas.
![]()
![]()
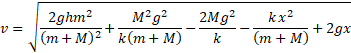
ODP. Otrzymane powyżej równanie opisuje szukaną zależność prędkości układu od wielkości odkształcenia sprężyny.
Dla wszystkich, którzy wolą obejrzeć i posłuchać jak rozwiązywać trudne zadania, polecamy film z tymże zadaniem na naszym kanale:
Zadanie 2. Zderzenie centralne idealnie sprężyste.
Dwie różne kule o masach m1 i m2 zderzają się centralnie idealnie sprężyście. Przed zderzeniem prędkości kul miały przeciwne zwroty i wynosiły v1 oraz v2. Wykaż, że po zderzeniu prędkości obu kul wyrażają się wzorami:
![]()
![]()
Rozwiązanie:
Podczas zderzeń centralnych jedyny kierunek ruchu to prosta łącząca środki obu kul. Wszystko rozwiązujemy w jednym wymiarze np. wzdłuż osi OX.

Podczas zderzeń idealnie sprężystych zachowane są dwie zasady: pędu i energii. Energia nie jest wektorem ale należy pamiętać, że pęd jest wektorem i podczas pisania równań ma znaczenie zwrot prędkości chwilowej.
![]() ZZE (1)
ZZE (1)
![]()
ZZP (2)
Z tych dwóch równań stworzymy układ, w którym jedynymi niewiadomymi są szukane prędkości kul po zderzeniu. Pierwsze równanie mnożymy obustronnie przez 2 i przenosimy wyrazy z masą pierwszą na lewą stronę a z masą drugą na prawą stronę. Grupowanie mas wykonujemy także dla drugiego równania.

![]()
![]()
Wyłączamy jednakowe masy przed nawias.
![]()
Jeżeli masy nie wynoszą zero i prędkości początkowe nie są jednakowe, to możemy podzielić stronami równanie pierwsze przez drugie.
![]()
Korzystając ze wzorów skróconego mnożenia otrzymujemy proste równanie.
![]()
![]()
Wyznaczamy wzór na prędkość drugiej kuli po zderzeniu i wstawiamy do drugiego równania, które dotyczyło zasady zachowanie pędu.
![]() (3)
(3)
![]()
![]()
![]()
![]() (4)
(4)
Wzór na prędkość pierwszej kuli po zderzeniu się zgadza. Teraz podstawiamy wzór (4) do (3).
![]()
Mnożymy obustronnie przez sumę mas i redukujemy wyrazy podobne.
![]()
![]()
![]()
Dzielimy przez sumę mas aby otrzymać szukaną postać.
![]() (5)
(5)
Otrzymane wzory (4) i (5) są identyczne z tezą postawioną w treści zadania. To kończy dowód.
