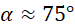Przyspieszenie całkowite jest sumą dwóch wektorów: przyspieszenia stycznego i dośrodkowego.
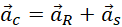
Przyspieszenie styczne, zgodnie z treścią zadania, jest stałe w czasie. Powoduje ono stały przyrost wartości prędkości liniowej pojazdu w ruchu na tym torze. Wartość tej prędkości zmienia wartość przyspieszenia dośrodkowego, które zależy wprost proporcjonalnie od kwadratu prędkości.
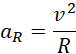
Promień toru nie ulega zmianie, więc tylko prędkość liniowa zmienia wartość aR. W pierwszej kolejności należy wyznaczyć prędkość uzyskaną po 15 sekundach rozpędzania.
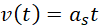
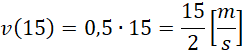
Wyznaczamy wartość przyspieszenia dośrodkowego dla tej chwili czasowej.
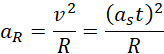
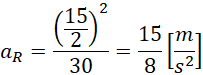
Jeżeli oba przyspieszenia: dośrodkowe i styczne są wzajemnie prostopadłe, to przyspieszenie całkowite można obliczyć na podstawie twierdzenia Pitagorasa.
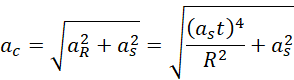
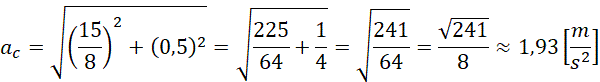
Do obliczenie kąta pomiędzy przyspieszeniem całkowitym a prędkością chwilową, wykorzystamy fakt, że prędkość chwilowa jest równoległa do przyspieszenia stycznego.
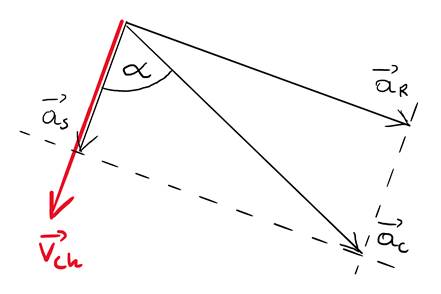
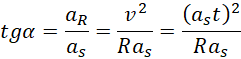

Sprawdzamy dla jakiego kąta tangens uzyskuje wartość 3,75.