Rozkładanie sił
Zadanie 1. Oświetlenie uliczne mocuje się często po przeciwnych stronach ulicy, na tej samej wysokości, do fasady przeciwległych budynków. Jeżeli odległość między przeciwległymi budynkami, na starówce pewnego miasta, wynosi 4 m, długość linki jest 5 m, a ciężar przymocowany na środku linki wynosi 60 N, to jaka siła wyrywa haki w kierunku poziomym?

Rozwiązanie:
Na hak mocujący linkę działa siła sprężystości (naprężenie). Szukana wartość jest składową poziomą naprężenia linki. Naprężenie linki jest na całej długości takie samo co do wartości. Zwrot wektora naprężenia tuż przy ścianie jest w stronę lampy ulicznej.
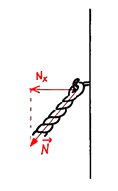
Zaznaczamy działające na zaczep oświetlenia siły. Ciężar może być dowolnej długości, ale naprężenia linek już nie.
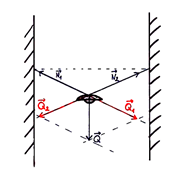
Wyznaczamy najpierw składowe wektora Q wzdłuż kierunku linek. Długości tych składowych są sobie równe, bo lampa wisi na środku. Naprężenia linek są, zgodnie z trzecią zasadą dynamiki, równe tym składowym ciężaru.
Rozkładamy teraz naprężenie na kierunek poziomy Nx oraz pionowy Ny.
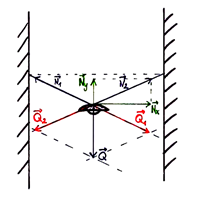
Można zauważyć podobieństwo między trójkątem sił Nx, Ny, N2 oraz trójkątem odległości
2 m, h, 2,5 m.
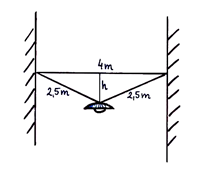
Dodatkowo widać, że składowa Ny jest równa połowie ciężaru Q, czyli 30 N. Układamy więc odpowiednie równanie.
![]()
Wyznaczamy z twierdzenia Pitagorasa wartość wysokości h trójkąta odległości.
![]()
![]()
Wstawiamy dane do proporcji wynikającej z podobieństwa.
![]()
![]()
Szukana wartość siły wyrywającej zaczep haka, mocującego linkę do ściany, jest składową poziomą naprężenia Nx.
ODP. Zaczep haka jest wyrywany siłą 40 N.
