Rozwiązanie:
Warto na schemacie obwodu zaznaczyć kierunek przepływu prądu i oznaczyć nazwy tych natężeń. Pamiętajmy, że zaznaczamy bieguny baterii. Następnie rozpoczynamy od źródła i w każdym z węzłów rozdzielamy prąd na kolejne składowe.
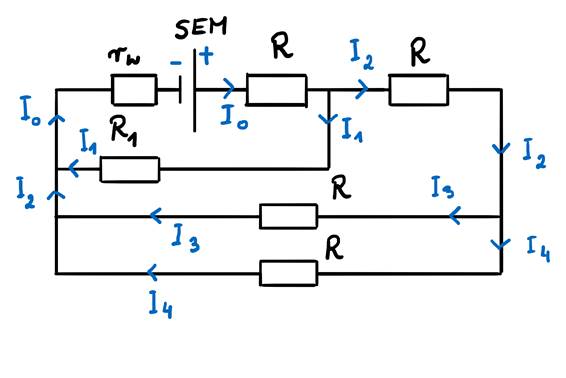
Do rozwiązania takiego zadania używamy I i II prawa Kirchhoffa. Pierwsze dotyczy rozgałęzień prądów a drugie dotyczy wzrostów i spadków napięć w obwodzie zamkniętym. Oznaczamy wszystkie węzły.
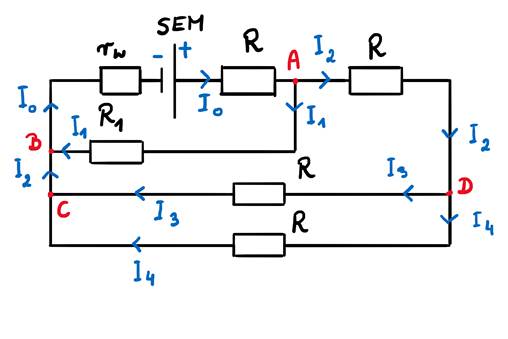
Punkty A i B oraz C i D dają dwa równania:
(1)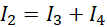
(2)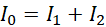
W naszym obwodzie widać trzy niezależne oczka prądowe. Zacznijmy od oczka zawierającego źródło prądu.
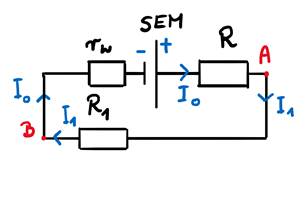
Zapisując napięcia (ich wzrosty i spadki) dla tego wycinka obwodu pamiętajmy, że opornik obniża napięcie a źródło podnosi.
(3)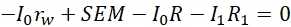
Przechodzimy do drugiego oczka prądowego.
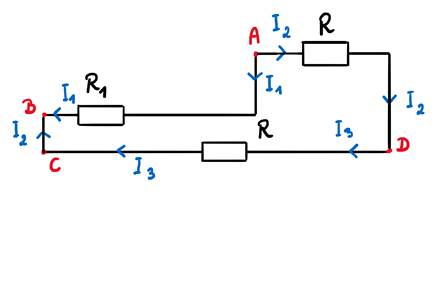
Idąc wokół tego wycinka obwodu zgodnie z ruchem wskazówek zegara przechodzimy przez oba oporniki R z prądem. Następuje tam spadek napięcia. W przypadku opornika R1 idziemy pod prąd, a więc jest tam skok napięcia.
(4)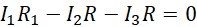
Pozostało jeszcze jedno oczko obwodu.
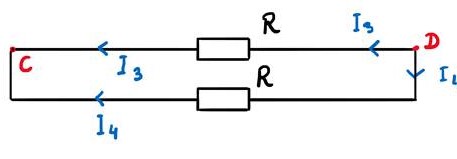
(5)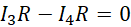
Wszystkie otrzymane równania spinamy klamrą. Tworzymy układ pięciu równań z pięcioma niewiadomymi.
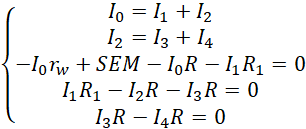
Z ostatniego równania wynika, że natężenie trzecie i czwarte jest równe sobie.
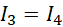
Mamy teraz układ czterech równań.
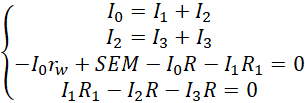
Redukujemy liczbę równań, korzystając z drugiego równania.
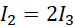
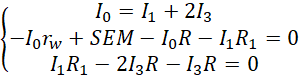
Pierwsze równanie pozwala sprowadzić układ już tylko do dwóch niewiadomych.
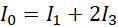
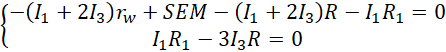
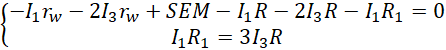
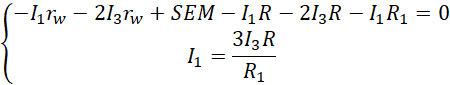
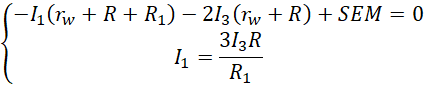
Ostatnie wyrażenie pozwala zastąpić natężenie pierwsze wielokrotnością natężenia trzeciego.
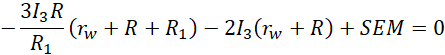
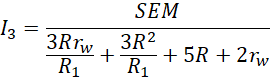
Wstawiamy wartości liczbowe i obliczamy trzecie natężenie.
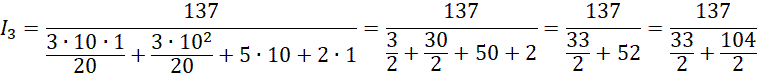
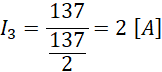
Czwarte natężenie jest takie same.

Obliczamy pozostałe natężenia.
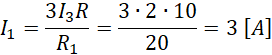
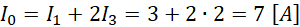
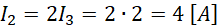
Odp. Natężenia wynoszą kolejno: I0 = 7A, I1 = 3A, I2 = 4A, I3 = 2A, I4 = 2A.