Hydrostatyka

Zadanie 1. Po powierzchni wody pływa styropianowa płyta o powierzchni dolnej S = 1,6 m², grubości h = 0,1 m i gęstości ρ = 400 kg/m³. Oblicz głębokość zanurzenia jeżeli na płycie spoczywa ciężar Q = 500 N.

Rozwiązanie:

Po sprawdzeniu czy wszystkie dane są z jednostkami układu SI, rysujemy schemat poglądowy.

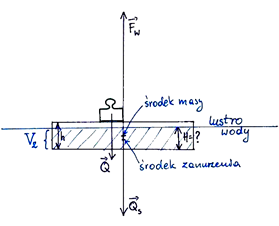
Przyjmujemy, oś układu odniesienia jest zwrócona ku górze. Oznacza to, że siła wyporu F_w jest dodatnia a ciężar styropianu Q_s i ciężar odważnika Q są ujemne. Jeżeli cały układ jest nieruchomy to przyspieszenie wypadkowe wynosi zero.

Wiemy, że masę można obliczyć jako iloczyn gęstości i objętości.

Objętość zanurzona zaznaczona jest na rysunku zakreskowaniem i oznaczona V_z, a objętość V to objętość całkowita.

lub zapis równoważny

Wstawiamy wartości liczbowe wraz z jednostkami.

ODP. Płyta styropianowa zanurza się na głębokość 7,125 cm.

Zadanie 2. W u-rurce znajdują się dwie, nie mieszające się ze sobą ciecze, o gęstościach ρ₁ = 1000 kg/m³ i ρ₂ = 1200 kg/m³. Oblicz różnicę wysokości słupków cieczy, jeżeli słupek cieczy pierwszej jest wysokości h₁ = 0,6 m, a cieczy drugiej jest objętościowo więcej.

Rozwiązanie:

Jeżeli jakaś ciecz ma mniejszą gęstość, to musi mieć wyższy słup do wytworzenia takiego samego ciśnienia.

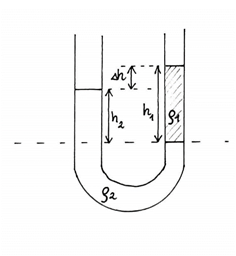
Przyjmiemy dolny poziom cieczy pierwszej jako poziom dla drugiego ramienia. Ciśnienie wywierane przez drugą ciecz, na tym poziomie, musi mieć taką samą wartość co wywierane przez cały słupek cieczy pierwszej. Jest to stwierdzenie wynikające z prawa Pascala.

Stosujemy wzór dla ciśnienia hydrostatycznego, które zależy tylko od wysokości słupa cieczy.

Po obu stronach równania ciśnień występuje przyspieszenie ziemskie i możemy przez g podzielić obustronnie.

Wyrażamy wysokość h₂ za pomocą h₁ i różnicy wysokości.

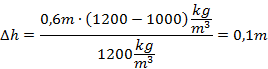
ODP. Słupek pierwszej cieczy jest wyższy od słupka drugiej cieczy o 10 cm.