Grawitacja

Zadanie 1. Znając promień orbity ziemskiej oraz okres obiegu Ziemi wokół Słońca, wyznacz masę Słońca.

Rozwiązanie:

Zapisujemy dane tablicowe: R = 1 AU = 150 mln km = 1,5∙10¹¹ m oraz T = 365,25 dni.

W ruchu po orbicie Ziemia porusza się pod wpływem siły grawitacji wytwarzanej przez Słońce. Jest to ruch w przybliżeniu po okręgu, więc siła grawitacji jest siłą dośrodkową. Zapisujemy wzór na przyspieszenie dośrodkowe i prędkość liniową w ruchu po okręgowe.

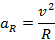
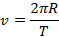
Wyznaczamy wartość siły dośrodkowej.

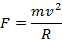
Podstawiamy prędkość do wzoru na siłę.

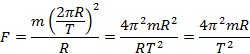
Jako siłę wstawiamy wzór na siłę grawitacji.

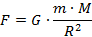
Po kilku przekształceniach otrzymujemy trzecie prawo Keplera.

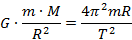
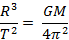
Wyznaczamy masę Słońca i podstawiamy wartości liczbowe (pamiętając o zamianie dni na sekundy).

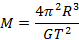
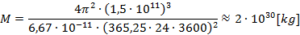
ODP. Masa Słońca wynosi około 2∙10³⁰ kg.

Zadanie 2. Wyprowadź wzór na gęstość Ziemi. Przyjmij, że dany jest promień R, przyspieszenie grawitacyjne na powierzchni g oraz stała grawitacyjna G.

Rozwiązanie:

Zapisujemy trzy potrzebne wzory:

– na gęstość materii ,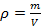

– na objętość kuli ,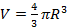

– na wartość przyspieszenia ziemskiego .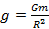

Podstawiamy wzór na objętość do wzoru na gęstość.

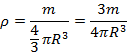
Ze wzoru na przyspieszenie wyznaczamy masę i podstawiamy do powyższego wzoru.

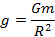
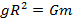
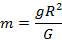
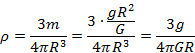
ODP. Gęstość Ziemi wyraża wzór 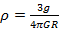.