Analiza danych pomiarowych

Podczas eksperymentów pojedynczy pomiar ma niepewność wynikającą z błędu przypadkowego lub systematycznego. Zmiana przyrządu odkryje czy był to błąd systematyczny, czyli z winy urządzenia pomiarowego. Co zrobić gdy winny jest „przypadek”? Może to eksperymentator źle odczytał wskazanie miernika, spojrzał pod złym kątem na podziałkę przyrządu. Zdarza się, że czynniki zewnętrzne nagle się zmieniły. Pojawił się podmuch powietrza, pomiary zagłuszone zostały przez hałasy, ktoś potrącił stolik z eksperymentem itp. Najlepszym wtedy sposobem jest wielokrotny pomiar.

Do analizy wielokrotnego pomiaru najlepiej użyć narzędzi statystycznych. Policzyć średnią arytmetyczną, odchylenie standardowe bądź błąd maksymalny i sporządzić histogram.

Przyjrzyjmy się jak wygląda pełna analiza na poniższym przykładzie. Zrobimy podsumowanie na dwa sposoby. Za pomocą błędu maksymalnego oraz za pomocą odchylenia standardowego.

Przykładowe doświadczenie. Podczas badania wahadła matematycznego uczniowie zmierzyli okres drgań dwadzieścia razy (tabela poniżej). Wyznacz wartość najbardziej prawdopodobną okresu wraz z błędem bezwzględnym. Następnie wyznacz błąd względny i oszacuj czy doświadczenie się udało.

Rozwiązanie:

W pierwszej kolejności najlepiej sporządzić histogram przedstawiający wyniki pomiaru.

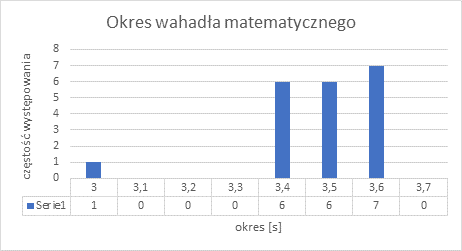
Jest to histogram dyskretny, gdzie każdy pomiar jest reprezentowany na wykresie. Przy zbliżonych pomiarach ten typ histogramu jest wygodny i pozwala łatwo odkryć odchylenia od normy (błędy grube). Jest to w tym przypadku pomiar o wartości 3,0, który w zdecydowany sposób odbiega od pozostałych wyników. Sprawdźmy jeszcze jak wyglądałby wykres za pomocą histogramu przedziałowego.

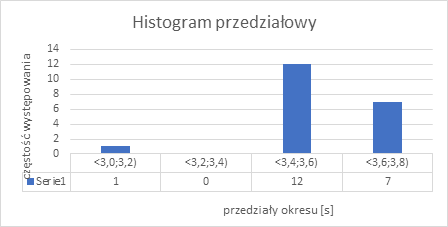
Przedziały w histogramie można dobierać dowolnie. Rozmiar będzie uzależniony od tego, jak rozbieżne są względem siebie pomiary.

Po wykonaniu histogramu przystępujemy do obliczenia średniej arytmetycznej.

We wzorze powyżej podane są wszystkie możliwe wersje symbolu średniej. Ostatnia wersja w postaci symbolu sumy używana jest dla skrócenia zapisu.

Do obliczenia średniej w naszym przykładzie warto użyć tylko pomiary od 3,4 do 3,6. Pomiar 3,0 traktujemy jako fluktuację (błąd gruby) i odrzucamy.

Do którego miejsca zaokrąglić? Jeśli nie używać narzędzi statystycznych (odchylenia standardowego) to można posługiwać się następującą zasadą: zawsze podajemy dwie cyfry znaczące w wyniku końcowym. Może warto wytłumaczyć o co chodzi. W przypadku, gdy wynik końcowy podamy tylko z jedną cyfrą znaczącą (np. 234,1 ≈ 200), to względne przybliżenie oscyluje od 5% do 50%. Jeżeli podamy dwie cyfry znaczące (np. 234,1 ≈ 230), to błąd względny zawiera się od 0,5% do 5%. W przypadku gdy weźmiemy trzy cyfry znaczące (np. 345.1 ≈ 234), otrzymamy przybliżenie z błędem w zakresie od 0,05% do 0,5%.

My obliczymy błąd bezwzględny i dopiero wtedy dokonamy zaokrąglenia średniej. W pierwszej kolejności wyliczymy błąd maksymalny, bo jest prostszy.

Wynik końcowy musimy zapisać od pierwszego miejsca po przecinku, bo tak narzuca nam niepewność maksymalna.

Błąd procentowy (względny) dla tego maksymalnego szacowania wynosi prawie 3%.

Teraz można oszacować odchylenie standardowe.

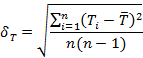
Przypominamy sobie, że błąd podajemy do pierwszej cyfry znaczącej, ale jeśli to jedynka, to podajemy następną cyfrę. Teraz można zapisać odpowiedź dla nowego rodzaju błędu.

Obliczamy również niepewność względną.

Wnioski:

1. Do wyliczenia wartości najbardziej prawdopodobnej z serii pomiarów używamy średniej arytmetycznej.
2. Odrzucamy błędy grube podczas analizy statystycznej.
3. Stosujemy błąd maksymalny, gdy wyniki niewiele się od siebie różnią.
4. Odchylenie standardowe daje zawsze mniejszy błąd względny niż błąd maksymalny.
5. Jeżeli niepewność względna jest poniżej 10%, to doświadczenie jest udane.
6. Jeżeli względna niepewność osiąga wartości poniżej 1%, to wynik eksperyment jest idealny.