Równania ruchu
Zadanie 1. Dwóch kolarzy trenuje na tej samej górze. Jeden z nich zjeżdża najpierw w dół stoku a potem podjeżdża. Drugi natomiast odwrotnie, najpierw wjeżdża a potem zjeżdża. Przyjmij, że punkt obserwacji znajduje się na szczycie, a kierunek osi x zwrócony jest w stronę podnóża góry. Pierwszy z kolarzy ruszył w dół stoku z przyspieszeniem a1 = 0,1 m/s2, na dole bez zatrzymywania natychmiast zawrócił i podjeżdżał z opóźnieniem 0,1 m/s2. Drugi z kolarzy rozpoczął podjazd z podnóża góry z prędkością v = 5 m/s i utrzymywał tę prędkość w czasie całego podjazdu. Po dojechaniu na szczyt zatrzymał się i rozpoczął zjazd z przyspieszeniem a2 = 0,05 m/s2. Do pierwszego spotkania doszło po 200 sekundach od równoczesnego rozpoczęcia jazdy przez cyklistów.
a) Wyznacz miejsce spotkania i długość stoku.
b) Wyznacz wartość prędkości względnej obu rowerzystów w chwili pierwszego spotkania.
c) Jak długo trwał trening pierwszego rowerzysty?
d) Ile czasu jechał drugi kolarz?
e) Określ jakim ruchem musiałby zjeżdżać, po dojechaniu na szczyt, pierwszy kolarz, aby spotkał się z drugim rowerzystą u podnóża góry. Podaj wartości parametrów, które określają rodzaj ruchu.
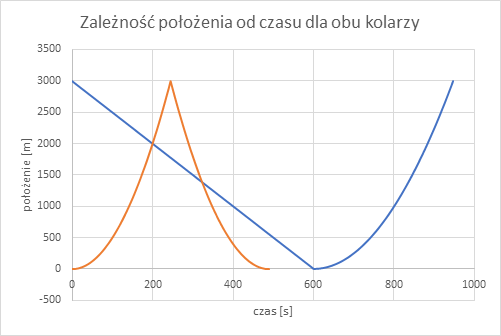
f) Napisz równania ruchu dla obu rowerzystów we wszystkich etapach ruchu. Narysuj na jednym wykresie zależność położenia od czasu dla każdego z cyklistów.
Rozwiązanie:
Zrobienie zadania po kolei nie jest często najlepszym pomysłem. Do wyliczenia czasu i miejsca spotkania najlepsze są równania ruchu, o które pytają dopiero w ostatnim podpunkcie. Przed rozwiązywaniem sporządzimy rysunek sytuacyjny. Jednostek na szczęście nie trzeba zamieniać.
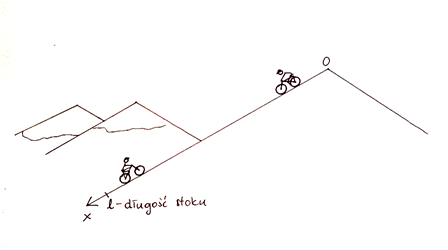
Nanieśmy początkowe wektory prędkości i przyspieszeń na nasz rysunek.
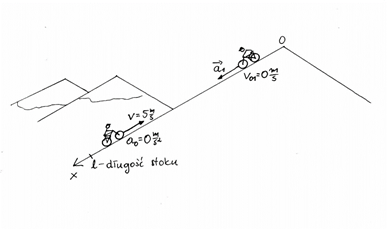
Na powyższym rysunku pokazane są różne sposoby podpisywania wektorów. Jeśli piszemy wartość to nie może być symbolu strzałki nad wielkością (v = 5 m/s). W przypadku gdy taka strzałka jest narysowana, to nie można napisać wartości tego wektora. Przed rozwiązywaniem przypomnijmy równanie ruchu i równanie prędkości.
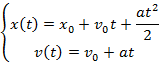
a) Zapiszemy równania ruchu i prędkości dla pierwszego etapu, czyli zjeżdżania pierwszego i podjazdu drugiego cyklisty.
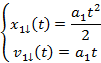
Strzałki pomogą nam zorientować się czy równanie dotyczy zjazdu czy podjazdu danego kolarza. Jeszcze spójrzmy na układ równań dla drugiego z nich.
![]()
Do spotkania dojdzie jeśli ich współrzędne położenia będą równe (nastąpi to oczywiści po czasie ts = 200 s).
![]()
![]()
Z tego równania można wyliczyć długość stoku.
![]()
Do obliczenia miejsca spotkania (xs) może posłużyć dowolne równanie ruchu.
![]()
b) W chwili mijania prędkości rowerzystów miały przeciwne zwroty. Wartość prędkości względnej jest więc sumą obu prędkości chwilowych.
![]()
![]()
c) Czas treningu pierwszego rowerzysty to czas zjazdu (t1) i czas podjazdu (t2). Do wyznaczenia czasu podjazdu potrzeba napisać równanie ruchu dla drugiego etapu.
![]()
Jako komentarz niech posłuży rysunek sytuacyjny z pierwszym kolarzem tuż po zawróceniu na dole.
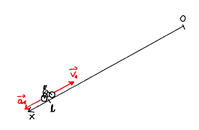
Dla pewności jednak przypomnijmy, że zwrot zgodny z osią obserwacji (osią układu) powoduje wartość dodatnią a zwrot przeciwny daje wartość ujemną.
Zacznijmy od obliczenia t1 podstawiając do odpowiedniego równania ruchu za x długość stoku, czyli l.
![]()
![]()
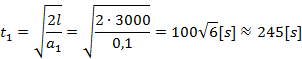
Jeśli chcemy wyliczyć z drugiej postaci równania ruchu czas dojechania na górę, to musimy za x wstawić zero.
![]()
Do obliczenia czasu podjazdu (t2) potrzeba znać v1, czyli prędkość z jaką rozpoczyna pierwszy kolarz drugi etap treningu. Można to ominąć zauważając, że ruch w dół miał taki sam wektor przyspieszenia jak ruch w górę. Oznacza to, że czas trwania przyspieszania od zera do v1 ma wartość taką samą jak czas trwania podjazdu, bo przyspieszanie i opóźnianie odbywa się na tej samej drodze.
![]()
d) Przypomnijmy równania ruchu i prędkości drugiego kolarza w czasie podjazdu.
![]()
Dopiszmy równania dla etapu drugiego (zjazdu), pamiętając, że kolarz zatrzymał się na górze i ruszył ruchem jednostajnie przyspieszonym.

W tym przypadku czas całkowity również składa się z dwóch czasów składowych. Czasu podjazdu t3 i czasu zjazdu t4. Podstawiając do równania ![]() za x wartość zero (szczyt góry) obliczymy czas t3.
za x wartość zero (szczyt góry) obliczymy czas t3.
![]()
![]()
Natomiast aby obliczyć czas zjazdu t4 musimy do odpowiedniego równania ruchu za x wstawić l = 3000 m.
![]()
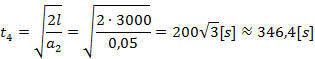
Sumujemy oba czasy i otrzymujemy całkowity czas treningu drugiego kolarza.
![]()
e) Pierwszy kolarz znalazł się na szczycie wzniesienia po około 490 s. Drugi znalazł się na dole po 946,4 s. Oznacza to, że pierwszy z nich musi w czasie 946,4-490=456,4 s zjechać ponownie w dół. Są dwie możliwości, albo zrobi to ruchem jednostajnym, albo jednostajnie przyspieszonym. Może oczywiście dowolnym rodzajem ruchu, ale w takim wypadku możliwości jest nieskończenie wiele. Pozostajemy przy dwóch typowych metodach zjazdu.
Dla ruchu jednostajnego za pomocą długości stoku i znanego czasu obliczymy prędkość.
![]()
![]()
Dla ruchu jednostajnie zmiennego sytuacja wygląda tak, że nie ma prędkości początkowej, a droga nadal jest długością stoku. Można wobec tego określić wartość przyspieszenia.
![]()
![]()
f) Przedstawimy najpierw równania ruchu dla pierwszego kolarza.
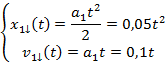
Jeżeli czas mierzylibyśmy ponownie od zera to w drugim etapie równania pierwszego kolarza wyglądałyby następująco.

Spójrzmy teraz na równania ruchu dla drugiego rowerzysty.
![]()
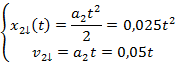
Widać, że wykresem położenia od czasu dla pierwszego cyklisty będą dwa fragmenty paraboli, bo ruch jest jednostajnie zmienny. Wykres dla drugiego z nich w pierwszej części będzie prostą, a potem fragmentem paraboli. W celu przedstawieniu wszystkich zależności na jednym wykresie należy uwzględnić przesunięcie w czasie dla drugich etapów. Należy odjąć od czasu długość trwania poprzedniego etapu.
![]()
![]()